When designing a new plant, predicting operating hours is essential for appropriately sizing equipment to achieve the target production. With the increasing complexity of process circuits, it becomes more challenging to estimate the operational hours for the entire plant. Each unit operation—whether it’s crushing, grinding, flotation, or dewatering—needs to be assessed not just for its own reliability, but also for its impact on the overall plant performance.
Reliability studies play a key role in this task by considering how individual unit operations affects overall plant uptime. To understand how reliability studies are structured, let’s explore some basic concepts.
Understanding System Components
A system consists of various components, which may include just one unit operations or entire operational areas. Each component is associated with operational states—either functioning, or in failure/maintenance.

Assessing system performance involves analyze some metrics. By measuring the intervals during which the system operates without failure and the time required to repair any issues that arise, we derive two key metrics: MTBF (Mean Time Between Failures) and MTTR (Mean Time to Repair). These metrics are crucial for understanding of the system’s reliability, availability, and maintainability.
MTBF
MTBF represents the average operational time between failures of repairable components. MTBF is a key indicator of reliability. For example, if a machine runs for 1000 hours before failing, and this occurs consistently, the MTBF is 1000 hours.
MTTR
MTTR measures the average time required to diagnose and repair equipment after a failure. It reflects the efficiency of maintenance operations and directly impacts system availability. For example, If a conveyor belt system experiences 200 hours of downtime across five repairs, the MTTR would be 40h (200h / 5 repairs).
Reliability, Availability and Maintainability
Reliability refers to the ability of a system to perform its intended functions over a specified period under set conditions. Availability, on the other hand, indicates the probability of a system being operational at any given time. While reliability focuses on performance consistency, availability emphasizes readiness and recovery from failures. Maintainability, meanwhile, is concerned with the ease and speed with which a system or component can be restored to working order after a failure.
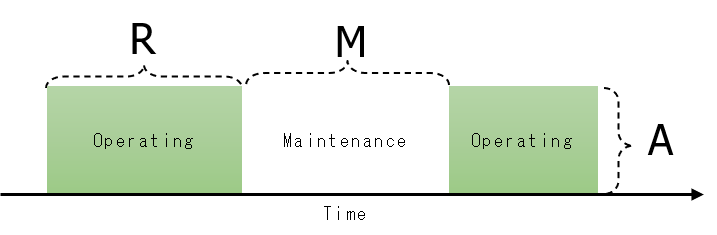
Reliability impacts availability because frequent failures reduce the time a system is operational. Maintainability impacts availability because quicker repairs mean the system can return to service faster. Together, these three concepts are crucial for understanding and optimizing overall system performance.
Reliability
Reliability (R(t)) is defined as the probability that a system will perform its intended function without failure over a specified time (t), under set conditions.
Mathematically, the reliability function is given by:
where:
- T represents the lifetime the system.
Availability
Availability (A) (or Inherent Availability) represents the probability that a system is operational at any given time. It is calculated using the formula:
where:
- MTBF is the average time the system operates without failure.
- MTTR is the average time taken to repair the system after a failure.
Maintainability
Maintainability (M) can be quantitatively expressed using the Mean Time to Repair (MTTR), which is a key metric that reflects the average time required to restore a system or component to operational status after a failure.
Failure rate and Bathtub curve
In addition to understanding the definitions of Reliability and Availability, it’s important to know the concepts of Failure Rate and it’s relation to reliability.
Failure Rate & Bathtub Curve
Failure rate, represented by λ (lambda), is a measure of the rate at which a system or component fails over time.

Along the lifetime of a system, the failure rate can change. The bathtub curve graphically represents the failure rate over the lifecycle of a component or system, consisting of three distinct phases:
- Infant Mortality: Characterized by a high initial failure rate due to manufacturing defects or early-life issues. Over time, this rate decreases as these issues are resolved.
- Useful Life: Features a low, constant failure rate, representing the stable operation period of the system. This is the optimal phase for most operations.
- Wear-Out: The failure rate increases as components age and wear out, leading to an increased likelihood of failure. Maintenance and replacements become crucial in this phase.
Reliability & Failure Rate
The reliability function R(t) is a probabilistic measure that describes the likelihood of a system, component, or piece of equipment functioning correctly, without failure, over a time interval t, under specified operating conditions.
Formal Definition
\(R(t) = P(T > t)\)Where:
- T is the random variable representing the time to failure (lifetime of the system).
- t is the specific time under consideration.
- P(T>t) is the probability that the time to failure exceeds t.
The reliability function is directly tied to the cumulative distribution function F(t), which represents the probability of failure occurring by time t:
\(F(t) = P(T \leq t)\)Thus:
\(R(t) = 1 – F(t)\)In cases where the failure rate (λ) is constant, the reliability function can directly relate
:
In essence, the reliability function R(t) is as a function of MTBF and provides a quantitative measure of a system’s operational dependability over time.
Reliability Block Diagram (RBD)
A Reliability Block Diagram (RBD) is a graphical representation of the logical interconnections of components within a system. In a mineral process scenario, it might be similar to the actual process flowsheet. RBD helps in breaking down complex systems into manageable parts for reliability analysis. Each block in the RBD represents a component or subsystem, and the arrangement of these blocks illustrates how the components are connected—whether in series, parallel, or a combination of both.
Series Configuration
In a series configuration, all components must function for the system to operate. If any component fails, the entire system fails. The reliability of a series system is the product of the reliabilities of its individual components.
Parallel Configuration
In a parallel configuration, the system functions as long as at least one component is operational. The reliability of a parallel system is higher because it can tolerate individual component failures.
:
Assessing system reliability through RBDs and analytical methods can be quite complex, particularly within large-scale industrial processes where components exhibit intricate interdependencies. To overcome these obstacles, professionals increasingly turn to sophisticated reliability analysis techniques and tools.
Limitations of RDB analysis for Mineral Process
In the context of a mineral process plant, the limitation of static analysis in RBDs becomes particularly evident due to the dynamic nature of the mineral process.
Buffer Dynamics: RBDs primarily focus on modeling component failures and their effects on system reliability. Buffers such as stockpiles, which primarily impact system availability through their capacity, is not be fully represented within traditional RBD frameworks.
Integrating buffers into RBDs requires clear definitions of how buffer states (full, empty, varying levels) influence overall system reliability and availability. For example, a stockpile may receive material from multiple conveyors or feeders and supply material to various processing units. Capturing these complex interactions in an RBD framework requires careful consideration of dependencies and feedback loops.This integration can be challenging without detailed data on buffer performance and operational conditions.
Static Analysis: RBDs provide a static snapshot of system reliability at a specific point in time, assuming constant conditions. They do not account well for dynamic changes in component reliability over time, varying operational conditions, or the impact of maintenance and repair activities.
Focus on Component Reliability: RBDs primarily model the reliability of individual components and their configurations (series, parallel, etc.), assuming components are either operational or failed. They do not explicitly account for states such as idle time where components are not actively contributing to system output.
Limited Scope of Analysis: RBDs primarily focus on reliability aspects related to component failures and their effects on overall system reliability. RBDs do not account for dynamic changes in material flow, process conditions, equipment interactions, and operational strategies.
Consider Dynamic Simulation
Replace traditional RBDs with dynamic simulation models that can capture the real-time behavior of buffers and their interactions with other system components. This approach allows for more accurate predictions of system reliability under varying operational scenarios.
